CART(Classification and Regression Tree)
CART的本质是对特征空间进行二元划分(即CART生成的决策树是一棵二叉树),它能够对类别变量和连续变量进行分裂,分割思路是先对某一维数据进行排序,然后对已经排好的特征进行切分,然后计算衡量指标(分类树用Gini指数,回归树用最小平方值),最后通过指标计算确定最后的划分点。
Gini指数
- 对于给定样本集D的Gini指数:分类问题中,假设有K个类,样本点属于第K类的概率为$p_k$,则概率分布的基尼指数为:$Gini(D)=\sum_{k=1}^K{p_k}{(1-p_k)}$
1.从Gini指数的数学形式中,可以得知,当$p_1=p_2=…=p_K$的时候Gini指数最大。
2.当某些$p_i$较大,即第$i$类的概率较大,样本类别不平衡,判别性较高。 - 在给定特征A的条件下,样本集合D的基尼指数为:$Gini(D,A)=p_1Gini(D_1)+p_2Gini(D_2)$,其中$p_i=\frac{D_i}{D_1+D_2}$,$i\in 1,2$
- 与信息熵的关系,信息熵定义为$Ent(D)=-\sum_{k=1}^K{p_k}{\log p_k}$,令$f(p_k)=-\log p_k \approx -\ln p_k$,对该式在$p=1$处做一阶泰勒展开,得到:带入信息熵的公式,可以得到和基尼系数一致的公式,也即是说基尼指数是信息熵中,$-\log p$在$p=1$处一阶泰勒展开后的结果!所以两者都可以用来度量数据集的纯度
Gini指数例子
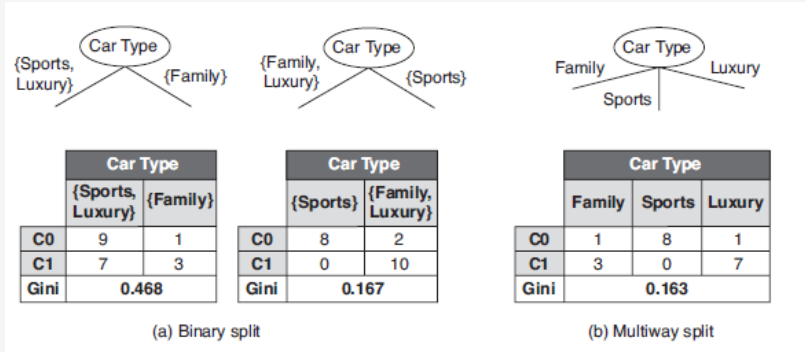
对于离散变量
数据集关于第一个特征维度的Gini指数的计算就是:
对于连续变量
因为连续变量的部分已经通过某一个值进行了划分,所以计算的时候和离散变量的计算类似