Bounding Box Regression with Uncertainty for Accurate Object Detection

概要

在目标检测数据集中，ground-truth bounding box在一些情况下经常会有一些内在的歧义。这些歧义通常来源于以下几个方面：a) 不准确的标记；b) 由于物体拥挤产生歧义；c) 物体本身的边界就存在歧义。本文提出了一个新的bbox regression loss。该loss将bounding box transformation与localization variance 联合学习。传统的bbox regression没有考虑ground truth bounding boxes的歧义性。此外，当分类分支的分数较高时，bbox regression 也被默认为是准确的。

方法

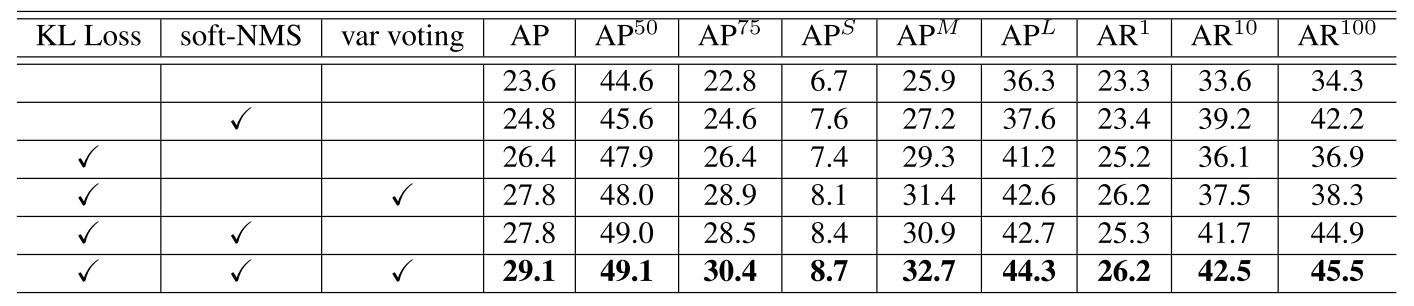
网络架构

bbox 参数化

不同于R-CNN系列算法对$(x,y,w,h)$进行回归，该文提出对$(x_1,y_1,x_2,y_2)$进行回归，参数化的定义如下所示：

$$t_{x1} = \frac{x_1-x_{1a}}{w_a},t_{x2}=\frac{x_2-x_{2a}}{w_a}\\ t_{y1} = \frac{y_1-y_{1a}}{h_a},t_{y2}=\frac{y_2-y_{2a}}{h_a}\\ t_{x1}^* = \frac{x_1^*-x_{1a}}{w_a},t_{x2}^*=\frac{x_2^*-x_{2a}}{w_a}\\ t_{y1}^* = \frac{y_1^*-y_{1a}}{h_a},t_{y2}^*=\frac{y_2^*-y_{2a}}{h_a}$$

接下来，该文假设坐标之间相互独立，为了简化期间，使用单变量的高斯分布：

$$P_\Theta(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x-x_e)^2}{2\sigma^2}}$$

其中$\Theta$是学习的参数，$x_e$是估计的bbox坐标，标准差$\sigma$度量估计的不确定性，当$\sigma\rightarrow0$时，意味着网络对于估计的bbox坐标相当确信。
真实框的bbox也能表达成一个高斯分布，当$\sigma\rightarrow0$时，该高斯分布转化为Dirac delta函数：

$$P_D(x)=\delta(x-x_g)$$

其中$x_g$是真实框的bbox坐标。

KL损失的bbox回归

从上述的描述可以得知，最终的目标是最小化$P_\Theta(x)$和$P_D(x)$的KL散度：

$$\hat{\Theta}=\mathop{\arg\min}\limits_{\Theta}\frac{1}{N}\sum{D_{KL}}({P_D(X)}\lVert{P_\Theta(x)})$$

因此当使用KL散度作为bbox regresssion时表示$L_{reg}$为:

$$\begin{eqnarray}L_{reg} &=&{D_{KL}}({P_D(X)}\lVert{P_\Theta(x)})\\ &=&\int P_D(X)\log{P_D(X)}\, dx - \int P_D(X)\log{P_\Theta(X)}\, dx\\ &=&\frac{(x_g-x_e)^2}{2\sigma^2}+\frac{\log{\sigma^2}}{2}+\frac{\log{2\pi}}{2}-H(P_D(x)) \end{eqnarray}$$

由于$\frac{\log{2\pi}}{2}$和$H(P_D(x))$和估计的参数$\Theta$无关，故：

$$L_{reg}\propto\frac{(x_g-x_e)^2}{2\sigma^2}+\frac{1}{2}\log{\sigma^2}$$

当$L_{reg}$对$\sigma$求导时，$\sigma$在分母位置，训练初期易出现梯度爆炸，所以为了解决这一问题，使用$a=\log{\sigma^2}$来代替$\sigma$的预测：

$$L_{reg}\propto\frac{e^{-a}}{2}{(x_g-x_e)^2}+\frac{1}{2}a$$

类似于smooth L1 loss中对$|x_g-x_e|>1$的处理，KL loss采用同样的处理方式：

$$L_{reg}\propto{e^{-a}}{(|x_g-x_e|-\frac{1}{2})}+\frac{1}{2}a$$

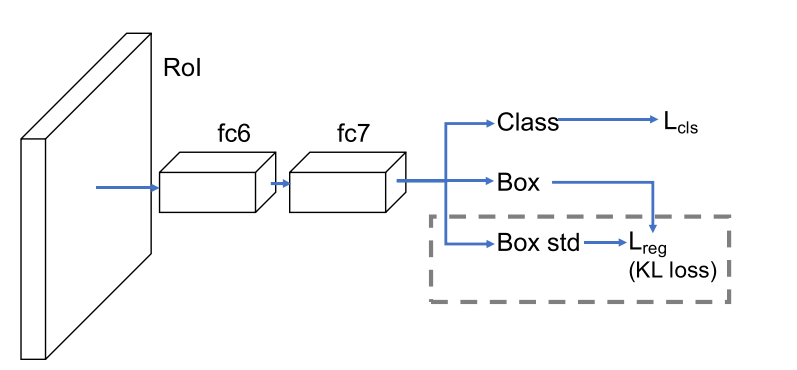
方差投票

最终的检测结果是一系列包含方差的bbox，为了获得更好的结果可以利用这些方差对近邻的bbox加权式的投票：

对接近最大分数bbox和最小方差的bbox赋予高权重，新的坐标计算如下所示：

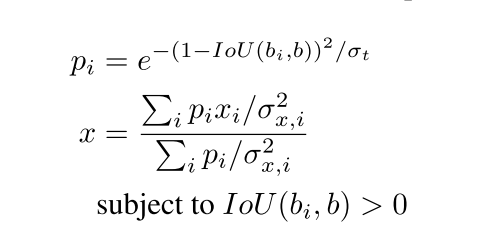
实验

消融实验