发表于 | 阅读次数:

特征工程

目的：将数据转换为更好的表示潜在问题的特征，从而提高机器学习性能

数据理解

目的：探索数据，了解数据，主要再EDA阶段完成

  1. 定性数据：
    • 定类：按名称分类—血型，城市
    • 定序：有序分类—成绩（A B C）
  2. 定量数据：
    • 定距： 可以加减—温度，日期
    • 定比： 可以乘除—价格，重量

数据清洗

目的：提高数据质量，降低算法用错误数据建模的风险

  1. 特征变换：模型无法处理或者不适合处理
    • 定性变量编码：Label Encoder, One-hot Encoder, Distribution Encoder
    • 标准化和归一化：z分数标准化（标准正态分布），min-max归一化
  2. 缺失值处理：增加不确定性，可能会导致不可靠输出
    • 不处理： 少量缺失样本
    • 删除： 大量样本缺失
    • 补全：（同类）均值/中位数/众数补全，高维映射（One-hot），模型预测，最邻近补全，矩阵补全（R-SVD）
  3. 异常值处理：减少脏数据
    • 简单统计：如describe()的统计描述，散点图等；
    • 3sigma法则（正态分布）/箱型图删除/截断；
    • 利用模型进行离群点检测：聚类，k近邻，one class SVM, Isolation Forest
  4. 其它：删除无效列/更改dtypes/删除列中的字符串/将时间戳从字符串转为日期格式等

特征构造

目的：增强数据表达，增加先验知识

  1. 统计量特征：计数，求和，比例，标准差
  2. 时间特征：绝对时间，相对时间，节假日，双休日
  3. 地理信息：分桶
  4. 非线性变换：取log/平方/根号
  5. 数据分桶：等频/等距分桶，best-ks分桶，卡方分桶
  6. 特征组合/特征交叉

特征选择

目的：平衡预测能力和计算复杂度，降低噪声

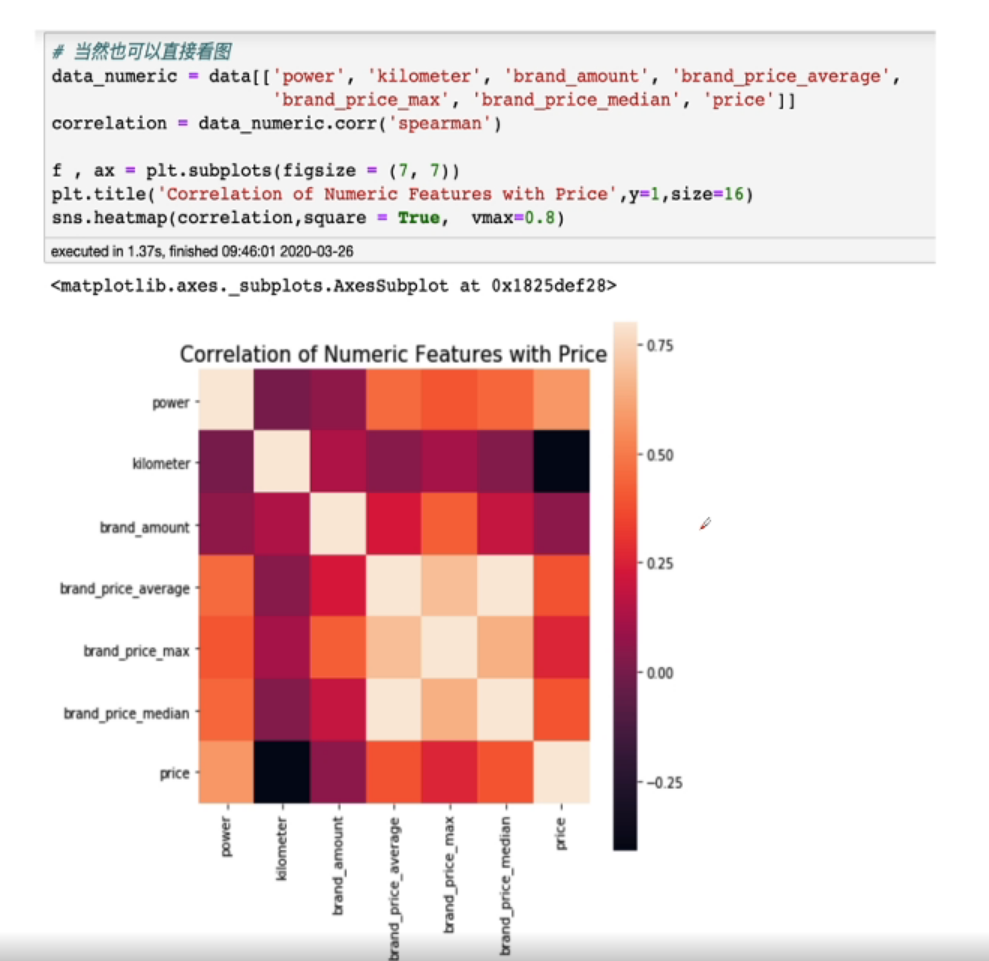
  1. 过滤式（Filter）：先利用特征选择方法对初识特征进行过滤然后再训练学习器，特征选择过程与后续学习器无关

    • Relief/方差选择/相关系数/卡方检验/互信息法

      方差越大，信息量越大，尽可能保留

  2. 包裹式（Wrapper）：直接把最终要使用的学习器的性能作为衡量特征子集的评价准则，其目的在于给定学习器选择最有利于其特征的特征子集

    • Las Vegas Wrapper（LVM）

  3. 嵌入式（Embedding）: 结合过滤式和包裹式方法，将特征选择与学习器训练过程融为一体，两者在同一优化过程中完成，即学习器训练过程中自动进行了特征选择

    • LR+L1或决策树

类别不平衡

  1. 扩充数据集

  2. 尝试其它评价指标：AUC等

  3. 调整theta值

    逻辑斯蒂回归，调整的是阈值，判断正负样本

  4. 重采样：过采样/欠采样

  5. 合成样本：SMOTE

  6. 选择其它模型：决策树等

  7. 加权少类别的样本错分代价

  8. 创新：

    • 将大类分解成多个小类
    • 将小类是为异常点，并用异常检测建模

代码部分

删除异常值（根据箱线图，将离群值删去）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 这里我包装了一个异常值处理的代码，可以随便调用。
def outliers_proc(data, col_name, scale=3):
    """
    用于清洗异常值，默认用 box_plot（scale=3）进行清洗
    :param data: 接收 pandas 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """

    def box_plot_outliers(data_ser, box_scale):
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())
    
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n

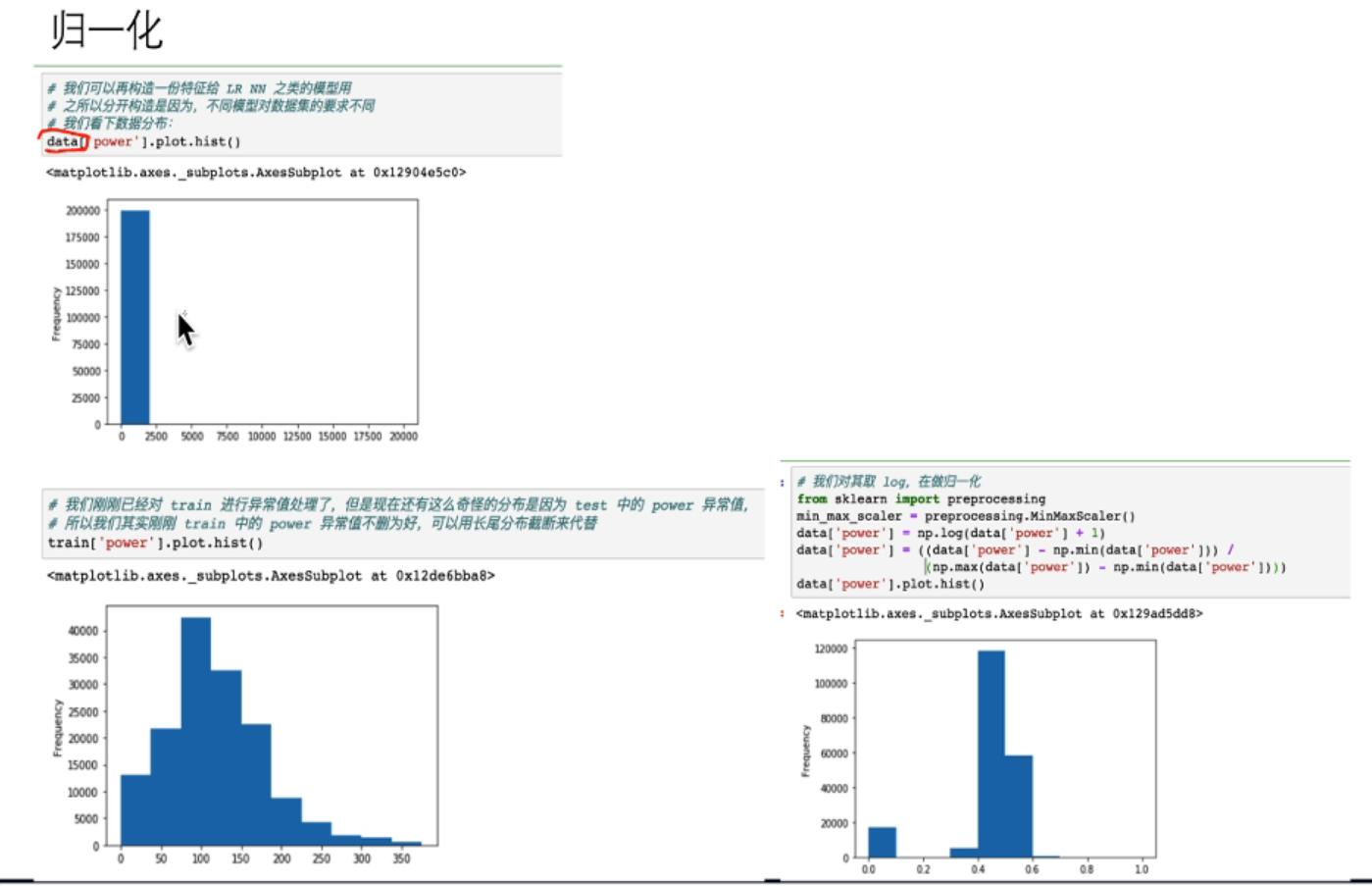
GPSQiQ.png

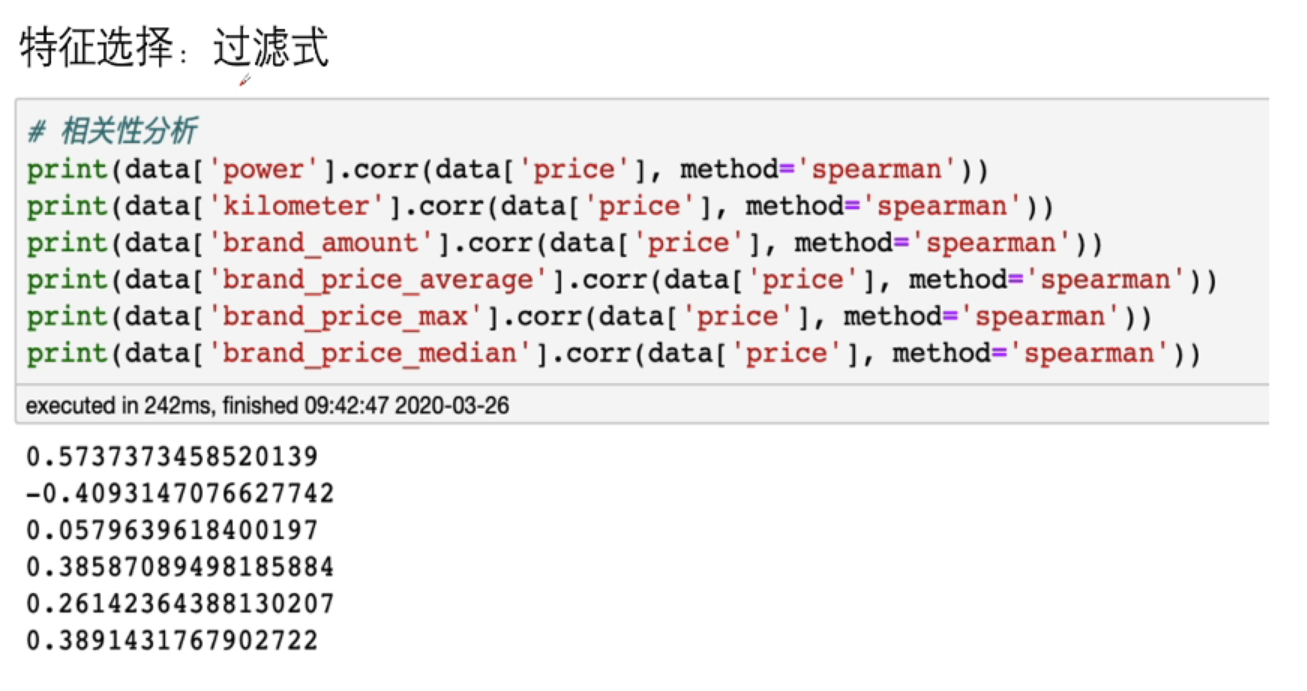
GPS6L6.png

采用spearman相关系数，因为他不要求数据是正态分布

GPS7OP.png

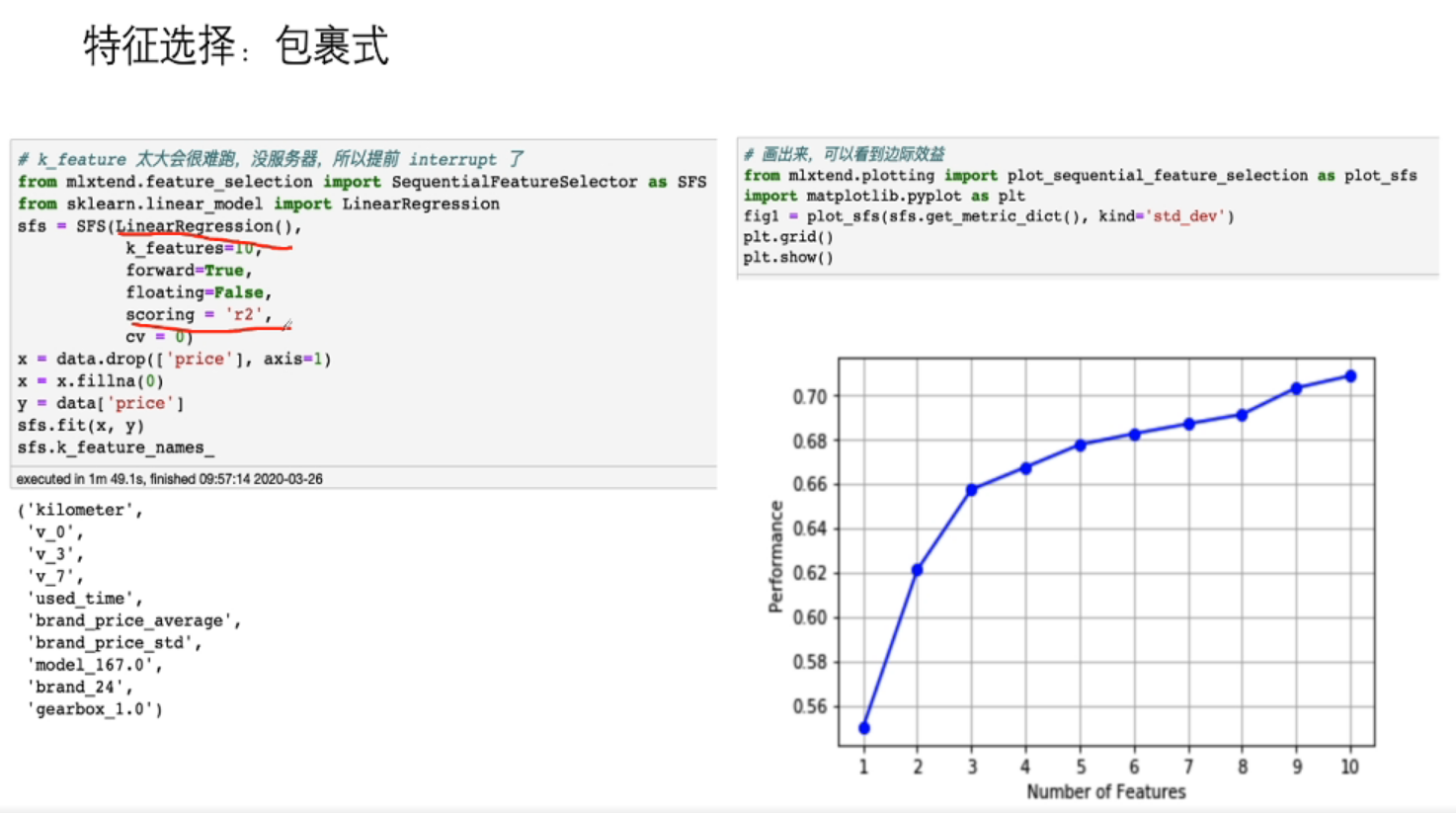
GPp9O0.png

Q&A

GPp8te.png

GP999H.png

经验总结

特征工程是比赛中最至关重要的的一块，特别的传统的比赛，大家的模型可能都差不多，调参带来的效果增幅是非常有限的，但特征工程的好坏往往会决定了最终的排名和成绩。

特征工程的主要目的还是在于将数据转换为能更好地表示潜在问题的特征，从而提高机器学习的性能。比如，异常值处理是为了去除噪声，填补缺失值可以加入先验知识等。

特征构造也属于特征工程的一部分，其目的是为了增强数据的表达。

有些比赛的特征是匿名特征，这导致我们并不清楚特征相互直接的关联性，这时我们就只有单纯基于特征进行处理，比如装箱，groupby，agg 等这样一些操作进行一些特征统计，此外还可以对特征进行进一步的 log，exp 等变换，或者对多个特征进行四则运算（如上面我们算出的使用时长），多项式组合等然后进行筛选。由于特性的匿名性其实限制了很多对于特征的处理，当然有些时候用 NN 去提取一些特征也会达到意想不到的良好效果。

对于知道特征含义（非匿名）的特征工程，特别是在工业类型比赛中，会基于信号处理，频域提取，丰度，偏度等构建更为有实际意义的特征，这就是结合背景的特征构建，在推荐系统中也是这样的，各种类型点击率统计，各时段统计，加用户属性的统计等等，这样一种特征构建往往要深入分析背后的业务逻辑或者说物理原理，从而才能更好的找到 magic。

当然特征工程其实是和模型结合在一起的，这就是为什么要为 LR NN 做分桶和特征归一化的原因，而对于特征的处理效果和特征重要性等往往要通过模型来验证。

总的来说，特征工程是一个入门简单，但想精通非常难的一件事。